Function for analyzing combined results of two concurrent diagnostic tests. Calculates post-test probabilities based on various scenarios (either test positive, both positive, both negative).
Usage
cotest(
test1_sens = 0.8,
test1_spec = 0.9,
test2_sens = 0.75,
test2_spec = 0.95,
indep = TRUE,
cond_dep_pos = 0.05,
cond_dep_neg = 0.05,
prevalence = 0.1,
fnote = FALSE,
fagan = FALSE,
preset = "custom"
)Arguments
- test1_sens
Sensitivity (true positive rate) of Test 1.
- test1_spec
Specificity (true negative rate) of Test 1.
- test2_sens
Sensitivity (true positive rate) of Test 2.
- test2_spec
Specificity (true negative rate) of Test 2.
- indep
Assume tests are conditionally independent (default is true).
- cond_dep_pos
Conditional dependence between tests for subjects with disease. Value between 0 (independence) and 1 (complete dependence).
- cond_dep_neg
Conditional dependence between tests for subjects without disease. Value between 0 (independence) and 1 (complete dependence).
- prevalence
Prior probability (disease prevalence in the population). Requires a value between 0.001 and 0.999.
- fnote
.
- fagan
.
- preset
Select a clinical preset or use custom values. Presets load evidence-based sensitivity and specificity values from medical literature with appropriate dependence parameters and prevalence estimates.
Value
A results object containing:
results$testParamsTable | a table | ||||
results$cotestResultsTable | a table | ||||
results$dependenceInfo | a html | ||||
results$dependenceExplanation | a html | ||||
results$explanation | a html | ||||
results$plot1 | an image |
Tables can be converted to data frames with asDF or as.data.frame. For example:
results$testParamsTable$asDF
as.data.frame(results$testParamsTable)
Examples
# Basic co-testing analysis with independent tests
cotest(
test1_sens = 0.80,
test1_spec = 0.90,
test2_sens = 0.75,
test2_spec = 0.95,
prevalence = 0.10,
indep = TRUE,
fagan = TRUE
)
#>
#> CO-TESTING ANALYSIS
#>
#> Test Parameters
#> ──────────────────────────────────────────────────────────────────────
#> Test Sensitivity Specificity Positive LR Negative LR
#> ──────────────────────────────────────────────────────────────────────
#> Test 1 80.00000 90.00000 8.000000 0.2222222
#> Test 2 75.00000 95.00000 15.000000 0.2631579
#> ──────────────────────────────────────────────────────────────────────
#>
#>
#> Co-Testing Results
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Scenario Post-test Probability Relative to Prevalence Post-test Odds
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Test 1 Positive Only 18.95735 1.89573460 0.233918129
#> Test 2 Positive Only 27.02703 2.70270270 0.370370370
#> Both Tests Positive 93.02326 9.30232558 13.333333333
#> Both Tests Negative 0.64558 0.06455778 0.006497726
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#>
#>
#> character(0)
#>
#> <div style="max-width: 800px;">
#>
#> Understanding Test Dependence in Diagnostic Testing
#>
#> What is conditional independence vs. dependence?
#>
#> Two diagnostic tests are conditionally independent if the result of
#> one test does not influence the result of the other test, *given the
#> disease status*. In other words, within the diseased population, the
#> probability of Test 1 being positive is not affected by knowing the
#> result of Test 2, and vice versa. The same applies within the
#> non-diseased population.
#>
#> Tests are conditionally dependent when the result of one test affects
#> the probability of the other test result, even when we know the
#> patient's true disease status.
#>
#> Mathematical Formulation
#>
#> Independent Tests: When tests are independent, joint probabilities are
#> simply the product of individual probabilities:
#>
#> P(Test1+ and Test2+ | Disease+) = P(Test1+ | Disease+) × P(Test2+ |
#> Disease+) = Sens₁ × Sens₂
#> P(Test1+ and Test2+ | Disease−) = P(Test1+ | Disease−) × P(Test2+ |
#> Disease−) = (1−Spec₁) × (1−Spec₂)
#> P(Test1− and Test2− | Disease+) = P(Test1− | Disease+) × P(Test2− |
#> Disease+) = (1−Sens₁) × (1−Sens₂)
#> P(Test1− and Test2− | Disease−) = P(Test1− | Disease−) × P(Test2− |
#> Disease−) = Spec₁ × Spec₂
#>
#> Dependent Tests: When tests are dependent, we adjust these
#> probabilities using a correlation parameter (denoted as ρ or ψ) that
#> ranges from 0 (independence) to 1 (maximum possible dependence):
#>
#> P(Test1+ and Test2+ | Disease+) = (Sens₁ × Sens₂) + ρᵨₒₛ × √(Sens₁ ×
#> (1−Sens₁) × Sens₂ × (1−Sens₂))
#> P(Test1+ and Test2+ | Disease−) = ((1−Spec₁) × (1−Spec₂)) + ρₙₑ𝑔 ×
#> √((1−Spec₁) × Spec₁ × (1−Spec₂) × Spec₂)
#>
#> Note: Similar adjustments are made for the other joint probabilities.
#>
#> When to Use Dependent vs. Independent Models
#>
#> Use the independence model when:
#>
#> Tests measure completely different biological phenomena
#> Tests use different biological specimens or mechanisms
#> You have no evidence of correlation between test results
#> You have limited information about how the tests interact
#>
#> Use the dependence model when:
#>
#> Tests measure the same or similar biological phenomena
#> Tests are based on the same biological specimen or mechanism
#> Previous studies indicate correlation between test results
#> Both tests are affected by the same confounding factors
#> You have observed that knowing one test result predicts the other
#>
#> Real-World Examples of Dependent Tests
#>
#> Two imaging tests (e.g., MRI and CT) looking at the same anatomical
#> structure
#> Two serological tests that detect different antibodies but against the
#> same pathogen
#> Tests that may both be affected by the same confounding factor (e.g.,
#> inflammation)
#> Multiple readings of the same test by different observers
#> Two different molecular tests detecting different genes of the same
#> pathogen
#>
#> Estimating Dependency Parameters
#>
#> The conditional dependence parameters (ρᵨₒₛ for diseased subjects and
#> ρₙₑ𝑔 for non-diseased subjects) ideally should be estimated from
#> paired testing data with known disease status. Values typically range
#> from 0 to 0.5 in practice, with higher values indicating stronger
#> dependence. When no data is available, sensitivity analyses using a
#> range of plausible values (e.g., 0.05, 0.1, 0.2) can reveal how much
#> dependence affects results.
#>
#> Impact of Ignoring Dependence
#>
#> Ignoring conditional dependence when it exists tends to:
#>
#> Overestimate the benefit of combined testing
#> Exaggerate post-test probabilities (either too high for positive
#> results or too low for negative results)
#> Produce unrealistically narrow confidence intervals
#> Lead to overly optimistic assessment of diagnostic accuracy
#>
#> Clinical Interpretation:
#>
#> Disease prevalence (pre-test probability): 10.0%
#>
#> Both tests positive: 93.0% probability (9.3x increase) - strong
#> evidence for disease
#>
#> Both tests negative: 0.6% probability (0.06x change) (major decrease)
#>
#> Single positive test:
#>
#>
#> Test 1 positive only: 19.0% (moderate increase)
#> Test 2 positive only: 27.0% (moderate increase)
#>
#> <div style='background-color: #f0f8ff; padding: 10px; border-radius:
#> 5px; margin-top: 15px;'>
#>
#>
#> Copy-ready summary:
#>
#> <p style='font-family: monospace; font-size: 12px;'>Co-testing with
#> Test 1 (sensitivity 80%, specificity 90%) and Test 2 (sensitivity 75%,
#> specificity 95%) in a population with 10.0% disease prevalence showed:
#> when both tests are positive, disease probability is 93.0% (9.3x
#> increase); when both are negative, disease probability is 0.6% (0.06x
#> decrease).
#>
#>
#> Warning: The `size` argument of `element_line()` is deprecated as of ggplot2 3.4.0.
#> ℹ Please use the `linewidth` argument instead.
#> ℹ The deprecated feature was likely used in the jmvcore package.
#> Please report the issue at <https://github.com/jamovi/jmvcore/issues>.
#>
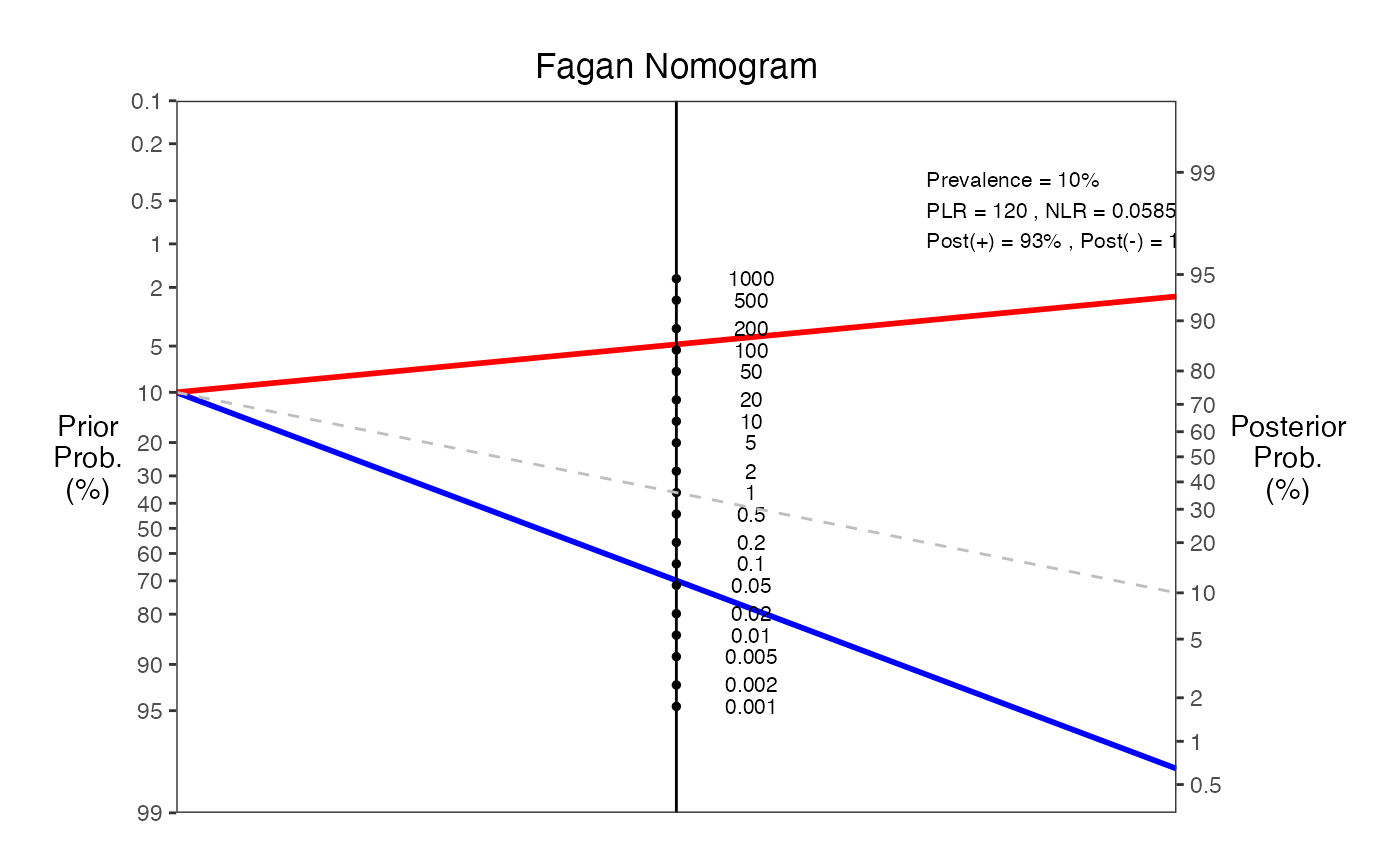
#> === Fagan Nomogram Results ===
#> Prevalence = 10%
#> Sensitivity = 94%
#> Specificity = 99%
#> Positive LR = 120
#> Negative LR = 0.0585
#> Post-test probability (positive test) = 93%
#> Post-test probability (negative test) = 1%
#> ===============================
 # Co-testing with dependent tests
cotest(
test1_sens = 0.85,
test1_spec = 0.88,
test2_sens = 0.82,
test2_spec = 0.92,
prevalence = 0.05,
indep = FALSE,
cond_dep_pos = 0.15,
cond_dep_neg = 0.10,
fnote = TRUE
)
#>
#> CO-TESTING ANALYSIS
#>
#> Test Parameters
#> ──────────────────────────────────────────────────────────────────────
#> Test Sensitivity Specificity Positive LR Negative LR
#> ──────────────────────────────────────────────────────────────────────
#> Test 1 85.00000 ᵃ 88.00000 ᵇ 7.083333 ᵈ 0.1704545 ᵉ
#> Test 2 82.00000 ᶠ 92.00000 ᵍ 10.250000 ᵈ 0.1956522 ᵉ
#> ──────────────────────────────────────────────────────────────────────
#> ᵃ Proportion of diseased patients correctly identified by Test 1
#> ᵇ Proportion of non-diseased patients correctly identified by
#> Test 1
#> ᵈ Positive Likelihood Ratio: how much more likely a positive
#> result is in diseased vs. non-diseased patients
#> ᵉ Negative Likelihood Ratio: how much more likely a negative
#> result is in diseased vs. non-diseased patients
#> ᶠ Proportion of diseased patients correctly identified by Test 2
#> ᵍ Proportion of non-diseased patients correctly identified by
#> Test 2
#>
#>
#> Co-Testing Results
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Scenario Post-test Probability Relative to Prevalence Post-test Odds
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Test 1 Positive Only 6.42043 ᵃ 1.28408660 ᵇ 0.068609347
#> Test 2 Positive Only 8.04881 ᵃ 1.60976225 ᵇ 0.087533520
#> Both Tests Positive 67.22155 ᵃ 13.44431051 ᵇ 2.050785129
#> Both Tests Negative 0.30503 ᵃ 0.06100646 ᵇ 0.003059656
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> ᵃ Probability of disease after obtaining this test result combination
#> ᵇ How many times more (or less) likely disease is after testing compared to before
#> testing
#>
#>
#> Tests are modeled with conditional dependence:
#>
#> Dependence for subjects with disease: 0.15
#>
#> Dependence for subjects without disease: 0.10
#>
#> Joint probabilities after accounting for dependence:
#>
#> P(Test1+,Test2+ | Disease+): 0.7176
#>
#> P(Test1+,Test2- | Disease+): 0.1324
#>
#> P(Test1-,Test2+ | Disease+): 0.1024
#>
#> P(Test1-,Test2- | Disease+): 0.0476
#>
#> P(Test1+,Test2+ | Disease-): 0.0184
#>
#> P(Test1+,Test2- | Disease-): 0.1016
#>
#> P(Test1-,Test2+ | Disease-): 0.0616
#>
#> P(Test1-,Test2- | Disease-): 0.8184
#>
#> <div style="max-width: 800px;">
#>
#> Understanding Test Dependence in Diagnostic Testing
#>
#> What is conditional independence vs. dependence?
#>
#> Two diagnostic tests are conditionally independent if the result of
#> one test does not influence the result of the other test, *given the
#> disease status*. In other words, within the diseased population, the
#> probability of Test 1 being positive is not affected by knowing the
#> result of Test 2, and vice versa. The same applies within the
#> non-diseased population.
#>
#> Tests are conditionally dependent when the result of one test affects
#> the probability of the other test result, even when we know the
#> patient's true disease status.
#>
#> Mathematical Formulation
#>
#> Independent Tests: When tests are independent, joint probabilities are
#> simply the product of individual probabilities:
#>
#> P(Test1+ and Test2+ | Disease+) = P(Test1+ | Disease+) × P(Test2+ |
#> Disease+) = Sens₁ × Sens₂
#> P(Test1+ and Test2+ | Disease−) = P(Test1+ | Disease−) × P(Test2+ |
#> Disease−) = (1−Spec₁) × (1−Spec₂)
#> P(Test1− and Test2− | Disease+) = P(Test1− | Disease+) × P(Test2− |
#> Disease+) = (1−Sens₁) × (1−Sens₂)
#> P(Test1− and Test2− | Disease−) = P(Test1− | Disease−) × P(Test2− |
#> Disease−) = Spec₁ × Spec₂
#>
#> Dependent Tests: When tests are dependent, we adjust these
#> probabilities using a correlation parameter (denoted as ρ or ψ) that
#> ranges from 0 (independence) to 1 (maximum possible dependence):
#>
#> P(Test1+ and Test2+ | Disease+) = (Sens₁ × Sens₂) + ρᵨₒₛ × √(Sens₁ ×
#> (1−Sens₁) × Sens₂ × (1−Sens₂))
#> P(Test1+ and Test2+ | Disease−) = ((1−Spec₁) × (1−Spec₂)) + ρₙₑ𝑔 ×
#> √((1−Spec₁) × Spec₁ × (1−Spec₂) × Spec₂)
#>
#> Note: Similar adjustments are made for the other joint probabilities.
#>
#> When to Use Dependent vs. Independent Models
#>
#> Use the independence model when:
#>
#> Tests measure completely different biological phenomena
#> Tests use different biological specimens or mechanisms
#> You have no evidence of correlation between test results
#> You have limited information about how the tests interact
#>
#> Use the dependence model when:
#>
#> Tests measure the same or similar biological phenomena
#> Tests are based on the same biological specimen or mechanism
#> Previous studies indicate correlation between test results
#> Both tests are affected by the same confounding factors
#> You have observed that knowing one test result predicts the other
#>
#> Real-World Examples of Dependent Tests
#>
#> Two imaging tests (e.g., MRI and CT) looking at the same anatomical
#> structure
#> Two serological tests that detect different antibodies but against the
#> same pathogen
#> Tests that may both be affected by the same confounding factor (e.g.,
#> inflammation)
#> Multiple readings of the same test by different observers
#> Two different molecular tests detecting different genes of the same
#> pathogen
#>
#> Estimating Dependency Parameters
#>
#> The conditional dependence parameters (ρᵨₒₛ for diseased subjects and
#> ρₙₑ𝑔 for non-diseased subjects) ideally should be estimated from
#> paired testing data with known disease status. Values typically range
#> from 0 to 0.5 in practice, with higher values indicating stronger
#> dependence. When no data is available, sensitivity analyses using a
#> range of plausible values (e.g., 0.05, 0.1, 0.2) can reveal how much
#> dependence affects results.
#>
#> Impact of Ignoring Dependence
#>
#> Ignoring conditional dependence when it exists tends to:
#>
#> Overestimate the benefit of combined testing
#> Exaggerate post-test probabilities (either too high for positive
#> results or too low for negative results)
#> Produce unrealistically narrow confidence intervals
#> Lead to overly optimistic assessment of diagnostic accuracy
#>
#> Clinical Interpretation:
#>
#> Disease prevalence (pre-test probability): 5.0%
#>
#> Both tests positive: 67.2% probability (13.4x increase) - strong
#> evidence for disease
#>
#> Both tests negative: 0.3% probability (0.06x change) (major decrease)
#>
#> Single positive test:
#>
#>
#> Test 1 positive only: 6.4% (slight increase)
#> Test 2 positive only: 8.0% (moderate increase)
#>
#> <div style='background-color: #f0f8ff; padding: 10px; border-radius:
#> 5px; margin-top: 15px;'>
#>
#>
#> Copy-ready summary:
#>
#> <p style='font-family: monospace; font-size: 12px;'>Co-testing with
#> Test 1 (sensitivity 85%, specificity 88%) and Test 2 (sensitivity 82%,
#> specificity 92%) in a population with 5.0% disease prevalence showed:
#> when both tests are positive, disease probability is 67.2% (13.4x
#> increase); when both are negative, disease probability is 0.3% (0.06x
#> decrease).
#>
#>
# High-stakes screening scenario
cotest(
test1_sens = 0.95,
test1_spec = 0.85,
test2_sens = 0.90,
test2_spec = 0.90,
prevalence = 0.02,
indep = TRUE,
fagan = TRUE,
fnote = TRUE
)
#>
#> CO-TESTING ANALYSIS
#>
#> Test Parameters
#> ───────────────────────────────────────────────────────────────────────
#> Test Sensitivity Specificity Positive LR Negative LR
#> ───────────────────────────────────────────────────────────────────────
#> Test 1 95.00000 ᵃ 85.00000 ᵇ 6.333333 ᵈ 0.05882353 ᵉ
#> Test 2 90.00000 ᶠ 90.00000 ᵍ 9.000000 ᵈ 0.11111111 ᵉ
#> ───────────────────────────────────────────────────────────────────────
#> ᵃ Proportion of diseased patients correctly identified by Test 1
#> ᵇ Proportion of non-diseased patients correctly identified by
#> Test 1
#> ᵈ Positive Likelihood Ratio: how much more likely a positive
#> result is in diseased vs. non-diseased patients
#> ᵉ Negative Likelihood Ratio: how much more likely a negative
#> result is in diseased vs. non-diseased patients
#> ᶠ Proportion of diseased patients correctly identified by Test 2
#> ᵍ Proportion of non-diseased patients correctly identified by
#> Test 2
#>
#>
#> Co-Testing Results
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Scenario Post-test Probability Relative to Prevalence Post-test Odds
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Test 1 Positive Only 1.41580 ᵃ 0.707898659 ᵇ 0.01436130
#> Test 2 Positive Only 1.06888 ᵃ 0.534441805 ᵇ 0.01080432
#> Both Tests Positive 53.77358 ᵃ 26.886792453 ᵇ 1.16326531
#> Both Tests Negative 1.333689e-4 ᵃ 0.006668445 ᵇ 1.333867e-4
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> ᵃ Probability of disease after obtaining this test result combination
#> ᵇ How many times more (or less) likely disease is after testing compared to before
#> testing
#>
#>
#> character(0)
#>
#> <div style="max-width: 800px;">
#>
#> Understanding Test Dependence in Diagnostic Testing
#>
#> What is conditional independence vs. dependence?
#>
#> Two diagnostic tests are conditionally independent if the result of
#> one test does not influence the result of the other test, *given the
#> disease status*. In other words, within the diseased population, the
#> probability of Test 1 being positive is not affected by knowing the
#> result of Test 2, and vice versa. The same applies within the
#> non-diseased population.
#>
#> Tests are conditionally dependent when the result of one test affects
#> the probability of the other test result, even when we know the
#> patient's true disease status.
#>
#> Mathematical Formulation
#>
#> Independent Tests: When tests are independent, joint probabilities are
#> simply the product of individual probabilities:
#>
#> P(Test1+ and Test2+ | Disease+) = P(Test1+ | Disease+) × P(Test2+ |
#> Disease+) = Sens₁ × Sens₂
#> P(Test1+ and Test2+ | Disease−) = P(Test1+ | Disease−) × P(Test2+ |
#> Disease−) = (1−Spec₁) × (1−Spec₂)
#> P(Test1− and Test2− | Disease+) = P(Test1− | Disease+) × P(Test2− |
#> Disease+) = (1−Sens₁) × (1−Sens₂)
#> P(Test1− and Test2− | Disease−) = P(Test1− | Disease−) × P(Test2− |
#> Disease−) = Spec₁ × Spec₂
#>
#> Dependent Tests: When tests are dependent, we adjust these
#> probabilities using a correlation parameter (denoted as ρ or ψ) that
#> ranges from 0 (independence) to 1 (maximum possible dependence):
#>
#> P(Test1+ and Test2+ | Disease+) = (Sens₁ × Sens₂) + ρᵨₒₛ × √(Sens₁ ×
#> (1−Sens₁) × Sens₂ × (1−Sens₂))
#> P(Test1+ and Test2+ | Disease−) = ((1−Spec₁) × (1−Spec₂)) + ρₙₑ𝑔 ×
#> √((1−Spec₁) × Spec₁ × (1−Spec₂) × Spec₂)
#>
#> Note: Similar adjustments are made for the other joint probabilities.
#>
#> When to Use Dependent vs. Independent Models
#>
#> Use the independence model when:
#>
#> Tests measure completely different biological phenomena
#> Tests use different biological specimens or mechanisms
#> You have no evidence of correlation between test results
#> You have limited information about how the tests interact
#>
#> Use the dependence model when:
#>
#> Tests measure the same or similar biological phenomena
#> Tests are based on the same biological specimen or mechanism
#> Previous studies indicate correlation between test results
#> Both tests are affected by the same confounding factors
#> You have observed that knowing one test result predicts the other
#>
#> Real-World Examples of Dependent Tests
#>
#> Two imaging tests (e.g., MRI and CT) looking at the same anatomical
#> structure
#> Two serological tests that detect different antibodies but against the
#> same pathogen
#> Tests that may both be affected by the same confounding factor (e.g.,
#> inflammation)
#> Multiple readings of the same test by different observers
#> Two different molecular tests detecting different genes of the same
#> pathogen
#>
#> Estimating Dependency Parameters
#>
#> The conditional dependence parameters (ρᵨₒₛ for diseased subjects and
#> ρₙₑ𝑔 for non-diseased subjects) ideally should be estimated from
#> paired testing data with known disease status. Values typically range
#> from 0 to 0.5 in practice, with higher values indicating stronger
#> dependence. When no data is available, sensitivity analyses using a
#> range of plausible values (e.g., 0.05, 0.1, 0.2) can reveal how much
#> dependence affects results.
#>
#> Impact of Ignoring Dependence
#>
#> Ignoring conditional dependence when it exists tends to:
#>
#> Overestimate the benefit of combined testing
#> Exaggerate post-test probabilities (either too high for positive
#> results or too low for negative results)
#> Produce unrealistically narrow confidence intervals
#> Lead to overly optimistic assessment of diagnostic accuracy
#>
#> Clinical Interpretation:
#>
#> Disease prevalence (pre-test probability): 2.0%
#>
#> Both tests positive: 53.8% probability (26.9x increase) - strong
#> evidence for disease
#>
#> Both tests negative: 0.0% probability (0.01x change) (major decrease)
#>
#> Single positive test:
#>
#>
#> Test 1 positive only: 1.4% (moderate decrease)
#> Test 2 positive only: 1.1% (moderate decrease)
#>
#> <div style='background-color: #f0f8ff; padding: 10px; border-radius:
#> 5px; margin-top: 15px;'>
#>
#>
#> Copy-ready summary:
#>
#> <p style='font-family: monospace; font-size: 12px;'>Co-testing with
#> Test 1 (sensitivity 95%, specificity 85%) and Test 2 (sensitivity 90%,
#> specificity 90%) in a population with 2.0% disease prevalence showed:
#> when both tests are positive, disease probability is 53.8% (26.9x
#> increase); when both are negative, disease probability is 0.0% (0.01x
#> decrease).
#>
#>
#>
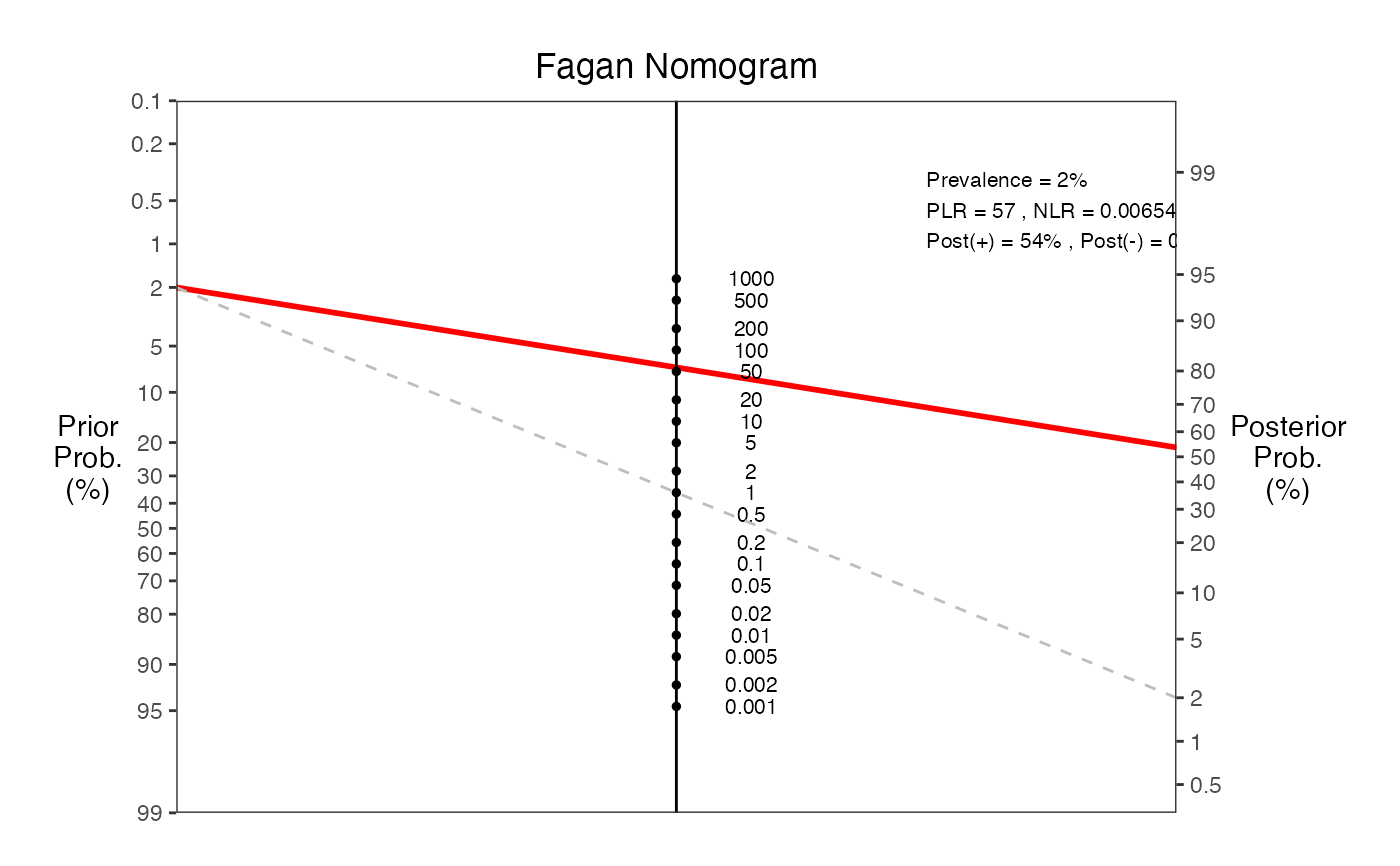
#> === Fagan Nomogram Results ===
#> Prevalence = 2%
#> Sensitivity = 99%
#> Specificity = 98%
#> Positive LR = 57
#> Negative LR = 0.00654
#> Post-test probability (positive test) = 54%
#> Post-test probability (negative test) = 0%
#> ===============================
# Co-testing with dependent tests
cotest(
test1_sens = 0.85,
test1_spec = 0.88,
test2_sens = 0.82,
test2_spec = 0.92,
prevalence = 0.05,
indep = FALSE,
cond_dep_pos = 0.15,
cond_dep_neg = 0.10,
fnote = TRUE
)
#>
#> CO-TESTING ANALYSIS
#>
#> Test Parameters
#> ──────────────────────────────────────────────────────────────────────
#> Test Sensitivity Specificity Positive LR Negative LR
#> ──────────────────────────────────────────────────────────────────────
#> Test 1 85.00000 ᵃ 88.00000 ᵇ 7.083333 ᵈ 0.1704545 ᵉ
#> Test 2 82.00000 ᶠ 92.00000 ᵍ 10.250000 ᵈ 0.1956522 ᵉ
#> ──────────────────────────────────────────────────────────────────────
#> ᵃ Proportion of diseased patients correctly identified by Test 1
#> ᵇ Proportion of non-diseased patients correctly identified by
#> Test 1
#> ᵈ Positive Likelihood Ratio: how much more likely a positive
#> result is in diseased vs. non-diseased patients
#> ᵉ Negative Likelihood Ratio: how much more likely a negative
#> result is in diseased vs. non-diseased patients
#> ᶠ Proportion of diseased patients correctly identified by Test 2
#> ᵍ Proportion of non-diseased patients correctly identified by
#> Test 2
#>
#>
#> Co-Testing Results
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Scenario Post-test Probability Relative to Prevalence Post-test Odds
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Test 1 Positive Only 6.42043 ᵃ 1.28408660 ᵇ 0.068609347
#> Test 2 Positive Only 8.04881 ᵃ 1.60976225 ᵇ 0.087533520
#> Both Tests Positive 67.22155 ᵃ 13.44431051 ᵇ 2.050785129
#> Both Tests Negative 0.30503 ᵃ 0.06100646 ᵇ 0.003059656
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> ᵃ Probability of disease after obtaining this test result combination
#> ᵇ How many times more (or less) likely disease is after testing compared to before
#> testing
#>
#>
#> Tests are modeled with conditional dependence:
#>
#> Dependence for subjects with disease: 0.15
#>
#> Dependence for subjects without disease: 0.10
#>
#> Joint probabilities after accounting for dependence:
#>
#> P(Test1+,Test2+ | Disease+): 0.7176
#>
#> P(Test1+,Test2- | Disease+): 0.1324
#>
#> P(Test1-,Test2+ | Disease+): 0.1024
#>
#> P(Test1-,Test2- | Disease+): 0.0476
#>
#> P(Test1+,Test2+ | Disease-): 0.0184
#>
#> P(Test1+,Test2- | Disease-): 0.1016
#>
#> P(Test1-,Test2+ | Disease-): 0.0616
#>
#> P(Test1-,Test2- | Disease-): 0.8184
#>
#> <div style="max-width: 800px;">
#>
#> Understanding Test Dependence in Diagnostic Testing
#>
#> What is conditional independence vs. dependence?
#>
#> Two diagnostic tests are conditionally independent if the result of
#> one test does not influence the result of the other test, *given the
#> disease status*. In other words, within the diseased population, the
#> probability of Test 1 being positive is not affected by knowing the
#> result of Test 2, and vice versa. The same applies within the
#> non-diseased population.
#>
#> Tests are conditionally dependent when the result of one test affects
#> the probability of the other test result, even when we know the
#> patient's true disease status.
#>
#> Mathematical Formulation
#>
#> Independent Tests: When tests are independent, joint probabilities are
#> simply the product of individual probabilities:
#>
#> P(Test1+ and Test2+ | Disease+) = P(Test1+ | Disease+) × P(Test2+ |
#> Disease+) = Sens₁ × Sens₂
#> P(Test1+ and Test2+ | Disease−) = P(Test1+ | Disease−) × P(Test2+ |
#> Disease−) = (1−Spec₁) × (1−Spec₂)
#> P(Test1− and Test2− | Disease+) = P(Test1− | Disease+) × P(Test2− |
#> Disease+) = (1−Sens₁) × (1−Sens₂)
#> P(Test1− and Test2− | Disease−) = P(Test1− | Disease−) × P(Test2− |
#> Disease−) = Spec₁ × Spec₂
#>
#> Dependent Tests: When tests are dependent, we adjust these
#> probabilities using a correlation parameter (denoted as ρ or ψ) that
#> ranges from 0 (independence) to 1 (maximum possible dependence):
#>
#> P(Test1+ and Test2+ | Disease+) = (Sens₁ × Sens₂) + ρᵨₒₛ × √(Sens₁ ×
#> (1−Sens₁) × Sens₂ × (1−Sens₂))
#> P(Test1+ and Test2+ | Disease−) = ((1−Spec₁) × (1−Spec₂)) + ρₙₑ𝑔 ×
#> √((1−Spec₁) × Spec₁ × (1−Spec₂) × Spec₂)
#>
#> Note: Similar adjustments are made for the other joint probabilities.
#>
#> When to Use Dependent vs. Independent Models
#>
#> Use the independence model when:
#>
#> Tests measure completely different biological phenomena
#> Tests use different biological specimens or mechanisms
#> You have no evidence of correlation between test results
#> You have limited information about how the tests interact
#>
#> Use the dependence model when:
#>
#> Tests measure the same or similar biological phenomena
#> Tests are based on the same biological specimen or mechanism
#> Previous studies indicate correlation between test results
#> Both tests are affected by the same confounding factors
#> You have observed that knowing one test result predicts the other
#>
#> Real-World Examples of Dependent Tests
#>
#> Two imaging tests (e.g., MRI and CT) looking at the same anatomical
#> structure
#> Two serological tests that detect different antibodies but against the
#> same pathogen
#> Tests that may both be affected by the same confounding factor (e.g.,
#> inflammation)
#> Multiple readings of the same test by different observers
#> Two different molecular tests detecting different genes of the same
#> pathogen
#>
#> Estimating Dependency Parameters
#>
#> The conditional dependence parameters (ρᵨₒₛ for diseased subjects and
#> ρₙₑ𝑔 for non-diseased subjects) ideally should be estimated from
#> paired testing data with known disease status. Values typically range
#> from 0 to 0.5 in practice, with higher values indicating stronger
#> dependence. When no data is available, sensitivity analyses using a
#> range of plausible values (e.g., 0.05, 0.1, 0.2) can reveal how much
#> dependence affects results.
#>
#> Impact of Ignoring Dependence
#>
#> Ignoring conditional dependence when it exists tends to:
#>
#> Overestimate the benefit of combined testing
#> Exaggerate post-test probabilities (either too high for positive
#> results or too low for negative results)
#> Produce unrealistically narrow confidence intervals
#> Lead to overly optimistic assessment of diagnostic accuracy
#>
#> Clinical Interpretation:
#>
#> Disease prevalence (pre-test probability): 5.0%
#>
#> Both tests positive: 67.2% probability (13.4x increase) - strong
#> evidence for disease
#>
#> Both tests negative: 0.3% probability (0.06x change) (major decrease)
#>
#> Single positive test:
#>
#>
#> Test 1 positive only: 6.4% (slight increase)
#> Test 2 positive only: 8.0% (moderate increase)
#>
#> <div style='background-color: #f0f8ff; padding: 10px; border-radius:
#> 5px; margin-top: 15px;'>
#>
#>
#> Copy-ready summary:
#>
#> <p style='font-family: monospace; font-size: 12px;'>Co-testing with
#> Test 1 (sensitivity 85%, specificity 88%) and Test 2 (sensitivity 82%,
#> specificity 92%) in a population with 5.0% disease prevalence showed:
#> when both tests are positive, disease probability is 67.2% (13.4x
#> increase); when both are negative, disease probability is 0.3% (0.06x
#> decrease).
#>
#>
# High-stakes screening scenario
cotest(
test1_sens = 0.95,
test1_spec = 0.85,
test2_sens = 0.90,
test2_spec = 0.90,
prevalence = 0.02,
indep = TRUE,
fagan = TRUE,
fnote = TRUE
)
#>
#> CO-TESTING ANALYSIS
#>
#> Test Parameters
#> ───────────────────────────────────────────────────────────────────────
#> Test Sensitivity Specificity Positive LR Negative LR
#> ───────────────────────────────────────────────────────────────────────
#> Test 1 95.00000 ᵃ 85.00000 ᵇ 6.333333 ᵈ 0.05882353 ᵉ
#> Test 2 90.00000 ᶠ 90.00000 ᵍ 9.000000 ᵈ 0.11111111 ᵉ
#> ───────────────────────────────────────────────────────────────────────
#> ᵃ Proportion of diseased patients correctly identified by Test 1
#> ᵇ Proportion of non-diseased patients correctly identified by
#> Test 1
#> ᵈ Positive Likelihood Ratio: how much more likely a positive
#> result is in diseased vs. non-diseased patients
#> ᵉ Negative Likelihood Ratio: how much more likely a negative
#> result is in diseased vs. non-diseased patients
#> ᶠ Proportion of diseased patients correctly identified by Test 2
#> ᵍ Proportion of non-diseased patients correctly identified by
#> Test 2
#>
#>
#> Co-Testing Results
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Scenario Post-test Probability Relative to Prevalence Post-test Odds
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> Test 1 Positive Only 1.41580 ᵃ 0.707898659 ᵇ 0.01436130
#> Test 2 Positive Only 1.06888 ᵃ 0.534441805 ᵇ 0.01080432
#> Both Tests Positive 53.77358 ᵃ 26.886792453 ᵇ 1.16326531
#> Both Tests Negative 1.333689e-4 ᵃ 0.006668445 ᵇ 1.333867e-4
#> ─────────────────────────────────────────────────────────────────────────────────────────────
#> ᵃ Probability of disease after obtaining this test result combination
#> ᵇ How many times more (or less) likely disease is after testing compared to before
#> testing
#>
#>
#> character(0)
#>
#> <div style="max-width: 800px;">
#>
#> Understanding Test Dependence in Diagnostic Testing
#>
#> What is conditional independence vs. dependence?
#>
#> Two diagnostic tests are conditionally independent if the result of
#> one test does not influence the result of the other test, *given the
#> disease status*. In other words, within the diseased population, the
#> probability of Test 1 being positive is not affected by knowing the
#> result of Test 2, and vice versa. The same applies within the
#> non-diseased population.
#>
#> Tests are conditionally dependent when the result of one test affects
#> the probability of the other test result, even when we know the
#> patient's true disease status.
#>
#> Mathematical Formulation
#>
#> Independent Tests: When tests are independent, joint probabilities are
#> simply the product of individual probabilities:
#>
#> P(Test1+ and Test2+ | Disease+) = P(Test1+ | Disease+) × P(Test2+ |
#> Disease+) = Sens₁ × Sens₂
#> P(Test1+ and Test2+ | Disease−) = P(Test1+ | Disease−) × P(Test2+ |
#> Disease−) = (1−Spec₁) × (1−Spec₂)
#> P(Test1− and Test2− | Disease+) = P(Test1− | Disease+) × P(Test2− |
#> Disease+) = (1−Sens₁) × (1−Sens₂)
#> P(Test1− and Test2− | Disease−) = P(Test1− | Disease−) × P(Test2− |
#> Disease−) = Spec₁ × Spec₂
#>
#> Dependent Tests: When tests are dependent, we adjust these
#> probabilities using a correlation parameter (denoted as ρ or ψ) that
#> ranges from 0 (independence) to 1 (maximum possible dependence):
#>
#> P(Test1+ and Test2+ | Disease+) = (Sens₁ × Sens₂) + ρᵨₒₛ × √(Sens₁ ×
#> (1−Sens₁) × Sens₂ × (1−Sens₂))
#> P(Test1+ and Test2+ | Disease−) = ((1−Spec₁) × (1−Spec₂)) + ρₙₑ𝑔 ×
#> √((1−Spec₁) × Spec₁ × (1−Spec₂) × Spec₂)
#>
#> Note: Similar adjustments are made for the other joint probabilities.
#>
#> When to Use Dependent vs. Independent Models
#>
#> Use the independence model when:
#>
#> Tests measure completely different biological phenomena
#> Tests use different biological specimens or mechanisms
#> You have no evidence of correlation between test results
#> You have limited information about how the tests interact
#>
#> Use the dependence model when:
#>
#> Tests measure the same or similar biological phenomena
#> Tests are based on the same biological specimen or mechanism
#> Previous studies indicate correlation between test results
#> Both tests are affected by the same confounding factors
#> You have observed that knowing one test result predicts the other
#>
#> Real-World Examples of Dependent Tests
#>
#> Two imaging tests (e.g., MRI and CT) looking at the same anatomical
#> structure
#> Two serological tests that detect different antibodies but against the
#> same pathogen
#> Tests that may both be affected by the same confounding factor (e.g.,
#> inflammation)
#> Multiple readings of the same test by different observers
#> Two different molecular tests detecting different genes of the same
#> pathogen
#>
#> Estimating Dependency Parameters
#>
#> The conditional dependence parameters (ρᵨₒₛ for diseased subjects and
#> ρₙₑ𝑔 for non-diseased subjects) ideally should be estimated from
#> paired testing data with known disease status. Values typically range
#> from 0 to 0.5 in practice, with higher values indicating stronger
#> dependence. When no data is available, sensitivity analyses using a
#> range of plausible values (e.g., 0.05, 0.1, 0.2) can reveal how much
#> dependence affects results.
#>
#> Impact of Ignoring Dependence
#>
#> Ignoring conditional dependence when it exists tends to:
#>
#> Overestimate the benefit of combined testing
#> Exaggerate post-test probabilities (either too high for positive
#> results or too low for negative results)
#> Produce unrealistically narrow confidence intervals
#> Lead to overly optimistic assessment of diagnostic accuracy
#>
#> Clinical Interpretation:
#>
#> Disease prevalence (pre-test probability): 2.0%
#>
#> Both tests positive: 53.8% probability (26.9x increase) - strong
#> evidence for disease
#>
#> Both tests negative: 0.0% probability (0.01x change) (major decrease)
#>
#> Single positive test:
#>
#>
#> Test 1 positive only: 1.4% (moderate decrease)
#> Test 2 positive only: 1.1% (moderate decrease)
#>
#> <div style='background-color: #f0f8ff; padding: 10px; border-radius:
#> 5px; margin-top: 15px;'>
#>
#>
#> Copy-ready summary:
#>
#> <p style='font-family: monospace; font-size: 12px;'>Co-testing with
#> Test 1 (sensitivity 95%, specificity 85%) and Test 2 (sensitivity 90%,
#> specificity 90%) in a population with 2.0% disease prevalence showed:
#> when both tests are positive, disease probability is 53.8% (26.9x
#> increase); when both are negative, disease probability is 0.0% (0.01x
#> decrease).
#>
#>
#>
#> === Fagan Nomogram Results ===
#> Prevalence = 2%
#> Sensitivity = 99%
#> Specificity = 98%
#> Positive LR = 57
#> Negative LR = 0.00654
#> Post-test probability (positive test) = 54%
#> Post-test probability (negative test) = 0%
#> ===============================